The concept of Multiscale Molecular Modeling?
Multiscale Molecular modelling and simulation combines methods that cover a range of lenght and time scales for the design of materials and bio systems. By definition, multiscale molecular modeling entails the application of computational techniques at two or more different length and time scale, which are often, but not always, dissimilar in their theoretical character due to the different pertaining scale. A distinction is made between the hierarchical approach, which involves running separate models with some sort of parametric coupling, and the hybrid approach, in which models are run concurrently over different spatial regions of a simulation. The relationships between different categories of methods commonly used in the multiscale modeling hierarchy are shown in the following Figure.
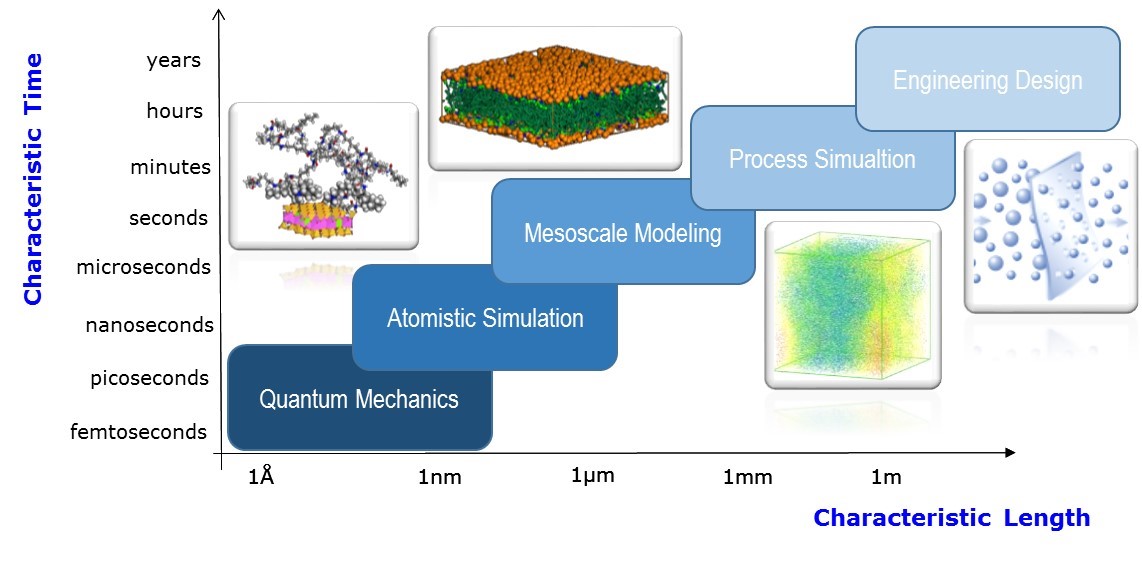
This figure evidences four characteristic time and length levels before reaching the last step, i.e. engineering design.
- the quantum scale, in which nuclei and electrons are the main players, and their quantum-mechanical state dictates the interactions among atoms. The possibility of obtaining data describing structural and electronic features of the system being considered and of taking into account effects associated with rupture and formation of chemical bonds in molecules, changes in electron configurations, and other similar phenomena are the main advantages of methods working at quantum scale.
- the atomistic scale. In atomistic simulations, all atoms are explicitly represented or in some cases, small groups of atoms are treated by single sites referred to as pseudo or united atoms. The potential energy in the system is estimated using a number of different classes of interactions (collectively known as force fields), typically consisting in: (i) bonded interactions, including bond-length (stretch) potentials, bond-angle (bend) potentials, torsion (twist) potentials and cross-terms, and (ii) non-bonded interactions, mostly comprising Coulomb interactions and dispersion forces.
- the mesoscopic scale. In these methods, a molecule is usually treated with a field description (field-based model) or microscopic particles (particle-based model) that incorporate molecular details implicitly. Therefore, they are able to simulate phenomena on length and time scales currently inaccessible by classical atomistic approach. At the simplest mesoscopic level, a polymer system may be modeled by a phenomenological expression for the free energy (field-based approach). For example, the Flory-Huggins or Landau free energies of mixing may be used to model aspects of polymer mixtures. In such models, the details of the system are incorporated into, e.g., the Flory parameter and the monomer segment mobility. Such phenomenological expressions are equivalent to truncated expansions of a more complicated free energy expression. Instead, in particle-based models the fluid is portrayed as a collection of point particles that represent lumps of fluid containing many molecules or segments of chains, termed beads. The interaction between beads is considered mesoscopic because the internal degrees of freedom of the fluid elements are ignored and only their center-of-mass motion is resolved.
- the macroscopic scale. At this level, constitutive laws govern the behavior of the physical system, which is considered as a continuous medium, ignoring discrete atomic and molecular structures and their influence on the overall system behavior. The basic assumption then consists in representing a heterogeneous material as an equivalent homogeneous one. A medium is called a continuum, if its volume contains an apparent continuity of material mass over the physical scale of the problem of interest. In general, this requires the domain of interest to be several orders of magnitude larger than the length scale of the elemental components. All mathematical functions (e.g., velocity or displacement fields) used to describe the state of the system are continuous, except possibly at a finite number of interior surfaces separating regions of continuity. Stress and strain tensors may be split into isotropic and deviatory parts, allowing to predict the behavior of the medium under both static and dynamic loading with separate descriptions of material constitutive behavior under hydrostatic and non-hydrostatic circumstances.
The following figure shows how the different scales are interrelated and evidences the information that is transferred from one scale to the other. Some methods and Software are also highlighted in the figure.
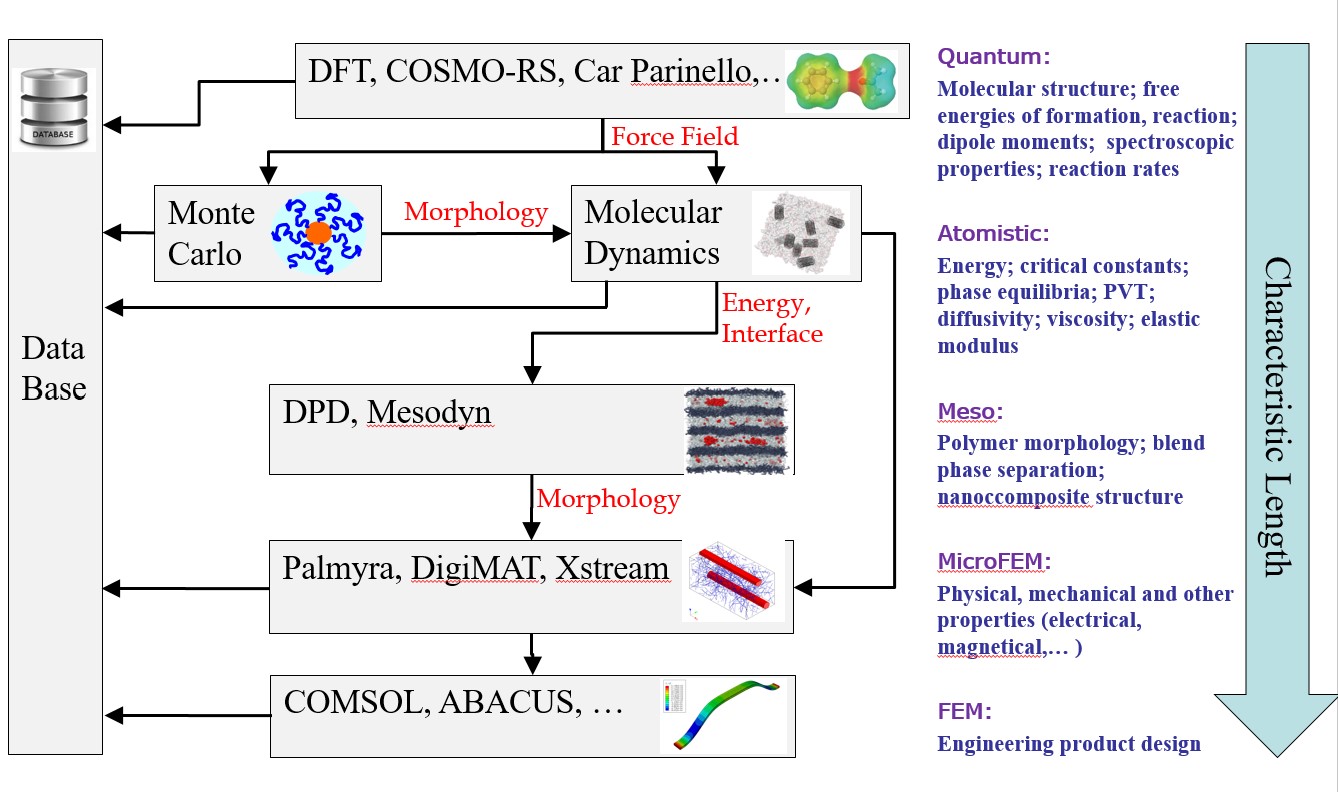
More information on Multiscale molecular modelling can be found in:
-
Scocchi et al., J. Phys. Chem. B, (2007), 111, 2143.
-
Toth R., Santese F., Pereira S.P., Romero-Nieto D., Pricl S., Fermeglia M., Posocco, Journal of Materials Chemistry, 22, 5398-5409 (2012) .
-
Pereira S.P, Scocchi G., Toth R., Posocco P., Romero-Nieto D., Pricl S., Fermeglia M., Journal of Multiscale Modeling, 3:151-176 (2012) .
Which are the applications of Multiscale Molecular Modelling?
The following figure summarizes some of the possible applications of multiscale molecular modelling in the fields of materials and life sciences.
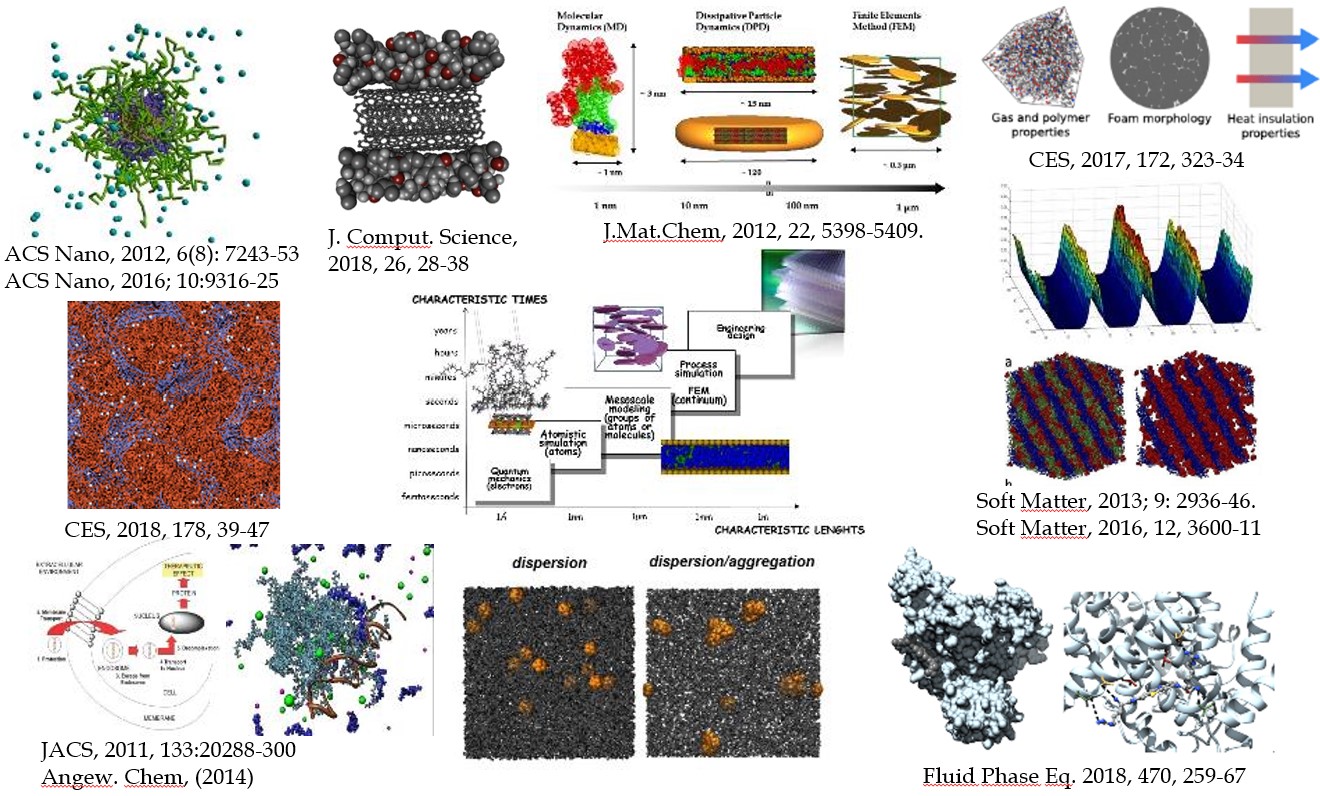
From the top left corner clockwise: (i) grafted silica nano particles design for bio applications, (ii) graphene based nano composites design, (iii) polymer clay nano composite design, (iv) design of thermoplastic polyurethane membranes for gas separation, (v) distribution of grafted gold nano particles in block co polymers, (vi) Mallard Blue binding to heparin and interaction with human serum albumin, (vii) dispersion of grafted silica nano particles in poly styrene, (viii) dendrons for gene therapy and (ix) design of plyurethane foams.